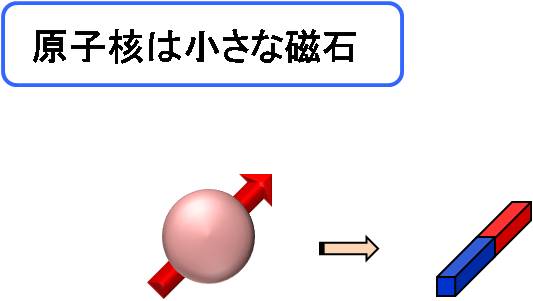
多くの原子核はスピンをもっており、磁気モーメントを有しています。 これは、小さな磁石とみなすことができます。 従って、核スピンはまわりの磁場と相互作用します。

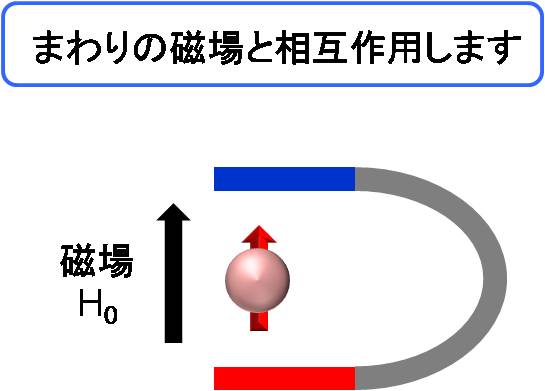
ただし、普通(古典論)と違うのはエネルギーが量子化されていることです。
例えばスピン量子数が1/2の場合、核スピンは磁場と相互作用し(ゼーマン相互作用)、
+1/2(上向きスピン)か-1/2(下向きスピン)のいずれかの状態となります。平衡状態では、
サンプル中のこれらの状態の数は、上向きスピンの方が下向きスピンに比べ、
僅かに多くなっています(ボルツマン分布)。
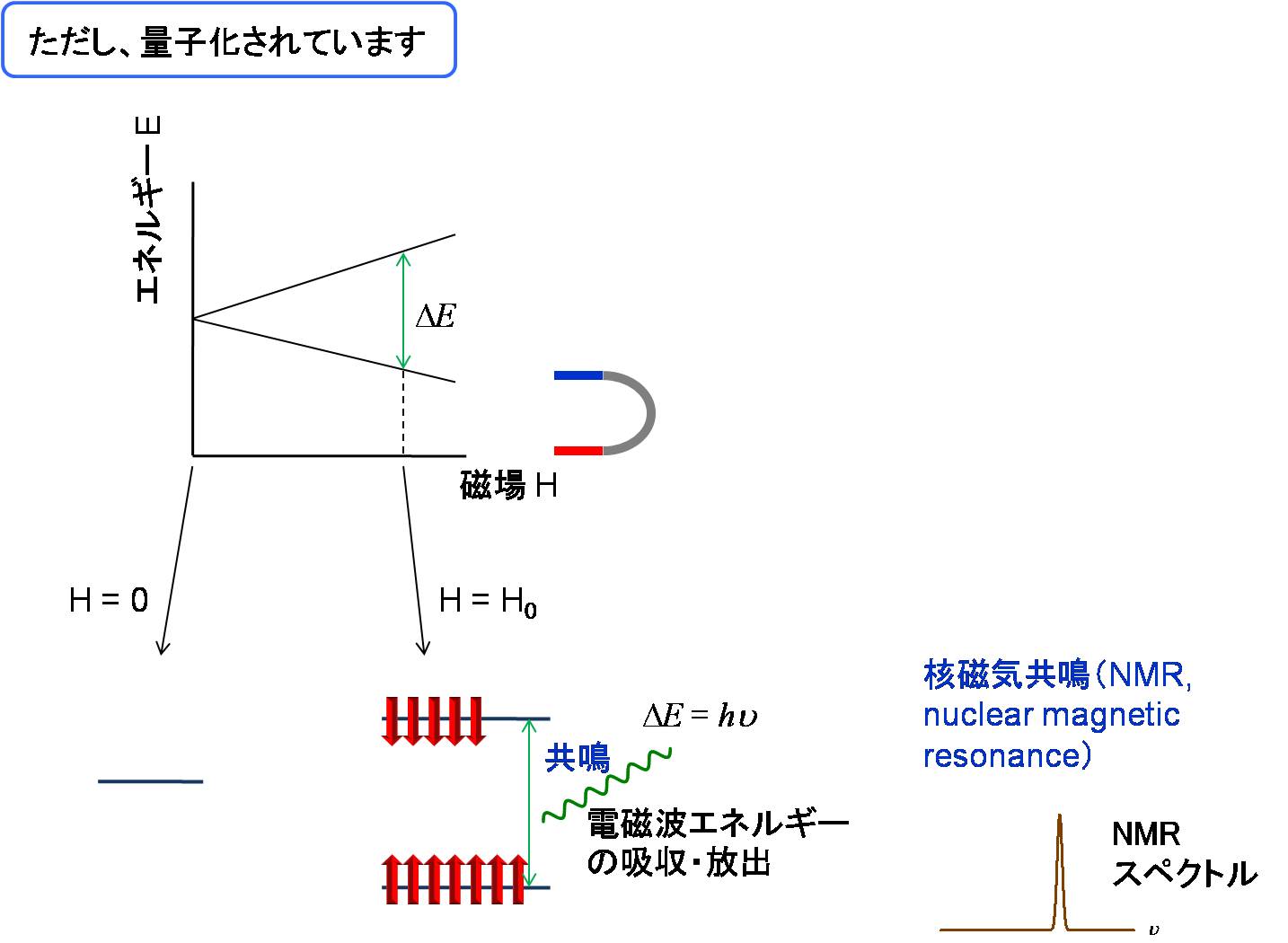
量子化された核スピンのエネルギーの差に相当する電磁波を照射すると、
エネルギーの吸収・放出(共鳴)が観測されます。
このように磁石を使って核スピンのエネルギーを調べる方法を核磁気共鳴(Nuclear Magnetic Resonance, NMR)法と言います。
尚、NMRで用いる電磁波は周波数が数10MHz - 1GHz程度のVHF-UHF帯域にある電磁波です。

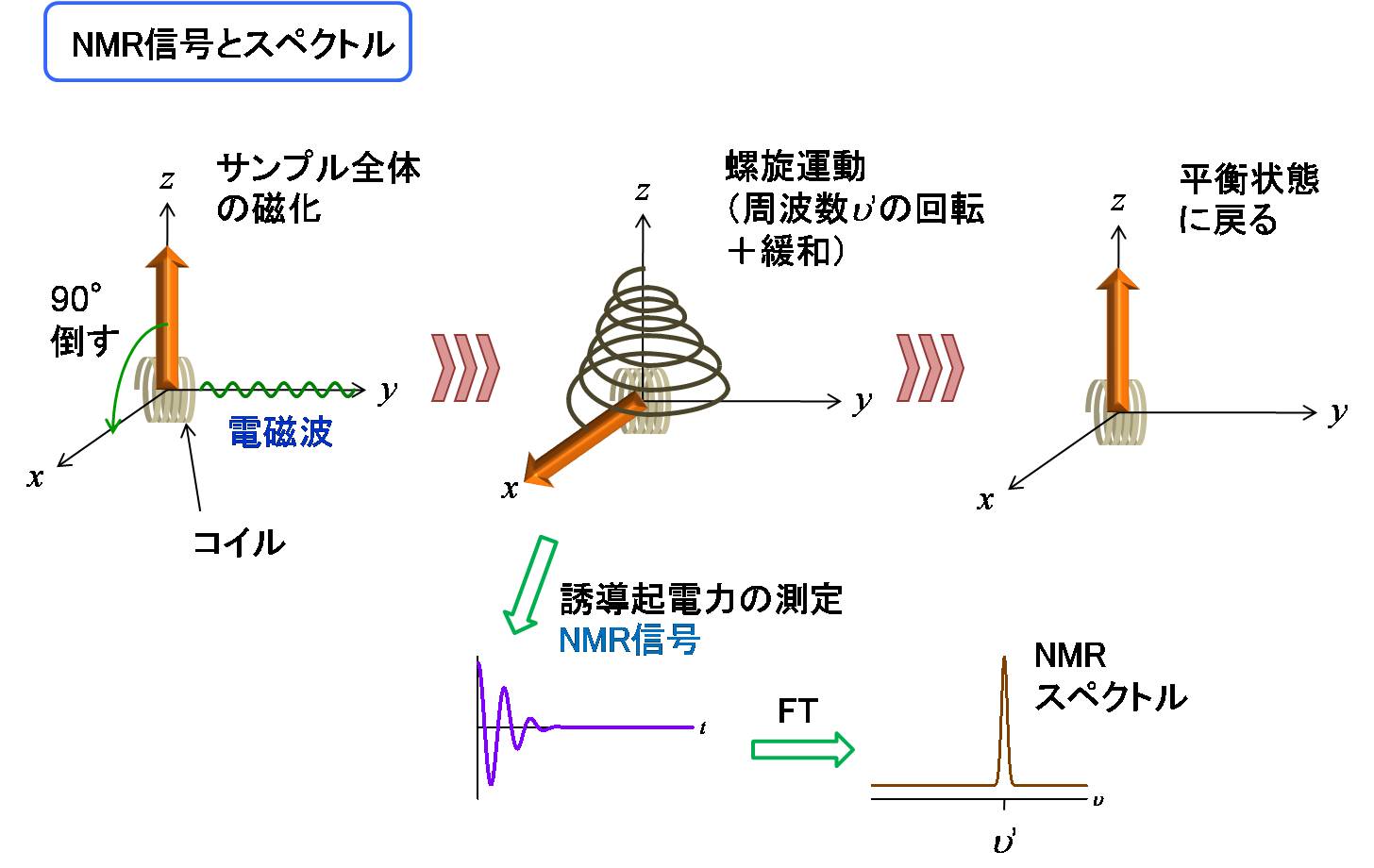
NMRスペクトルはどのように得られるのでしょうか?
個々の核スピンの大きさは非常に小さく、我々が対象とするのはサンプル全体の磁化です。
上向きスピンの方が下向きスピンに比べ少し多いので、全体の磁化はz方向(磁場H0)
を向いています(熱平衡状態)。これにΔEに相当する電磁波(MHz帯のラジオ波領域)を照射します。
下図のようにy方向から電磁波を照射すると、磁化はy軸周りに回転しするので、
磁化がx軸を向いたところで照射を止めます。
するとx軸を向いた磁化は螺旋運動をして熱平衡状態へと戻ります。この時、
螺旋の回転の周波数(ν')が原子核のおかれた環境に依存したものとなります。
この螺旋運動はコイルに誘導起電力を発生させます。この起電力がNMR信号です。
得られた信号をフーリエ変換すればNMRスペクトルが得られます。
核スピンは磁場と相互作用する(ゼーマン相互作用)ことを1.で見ましたが、 実際には、原子核のおかれた環境に応じて様々な相互作用をしています。 それらの相互作用によって線形が決まるNMRスペクトルは、 分子の構造を反映したものとなります。
相互作用としては、化学シフト相互作用、間接核スピン相互作用、 磁気双極子相互作用などがあります。
化学シフトは分子中の核のNMR周波数が、核のおかれた環境によりシフトすることです。 原子核のまわりにある電子は、磁場H0の下ではラーモアの運動をしており、 この回転運動により電流Iが発生し、核スピンの位置に反磁性磁場Hsが作られます。 このため、核スピンが受ける磁場はH = H0 + Hs となり共鳴位置がシフトします。
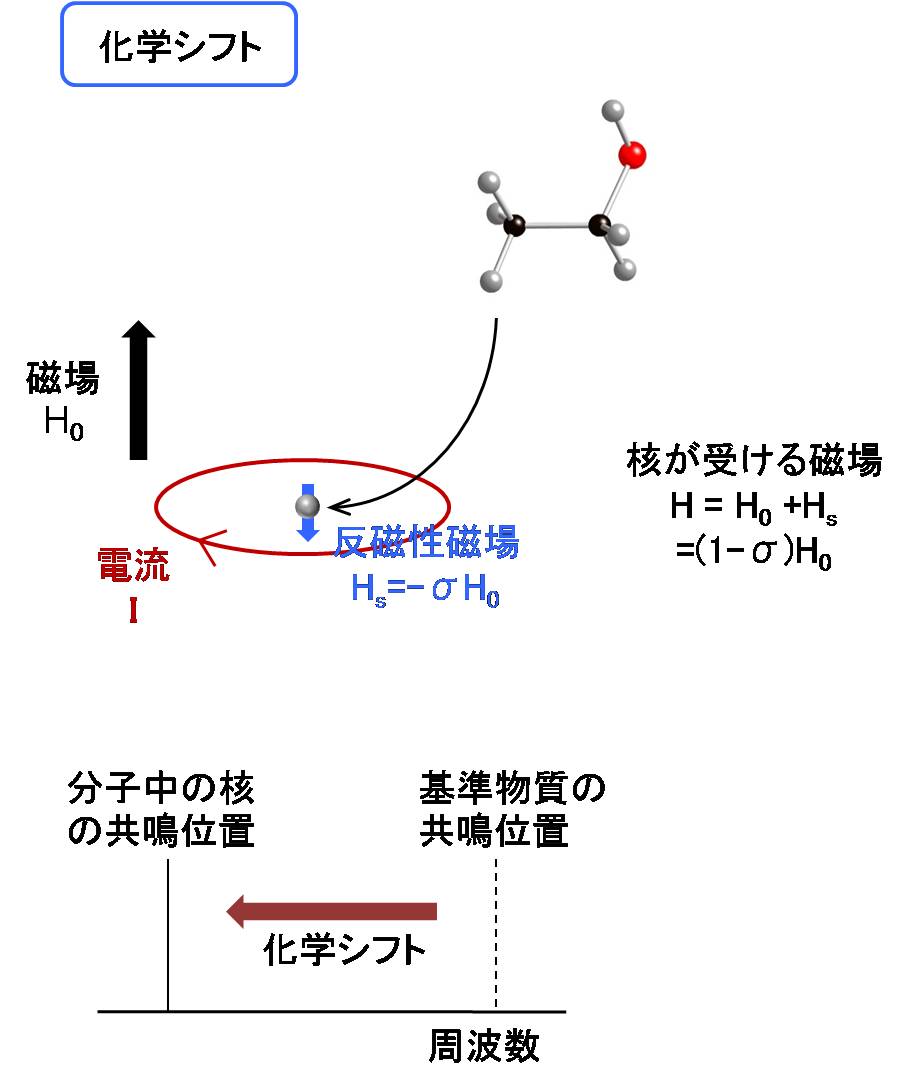
尚、化学シフトは次のように基準物質のピークからのずれをppm単位で表すことが多い。
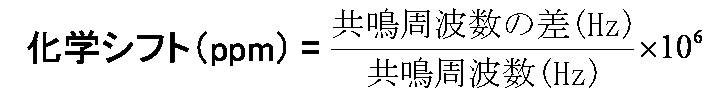
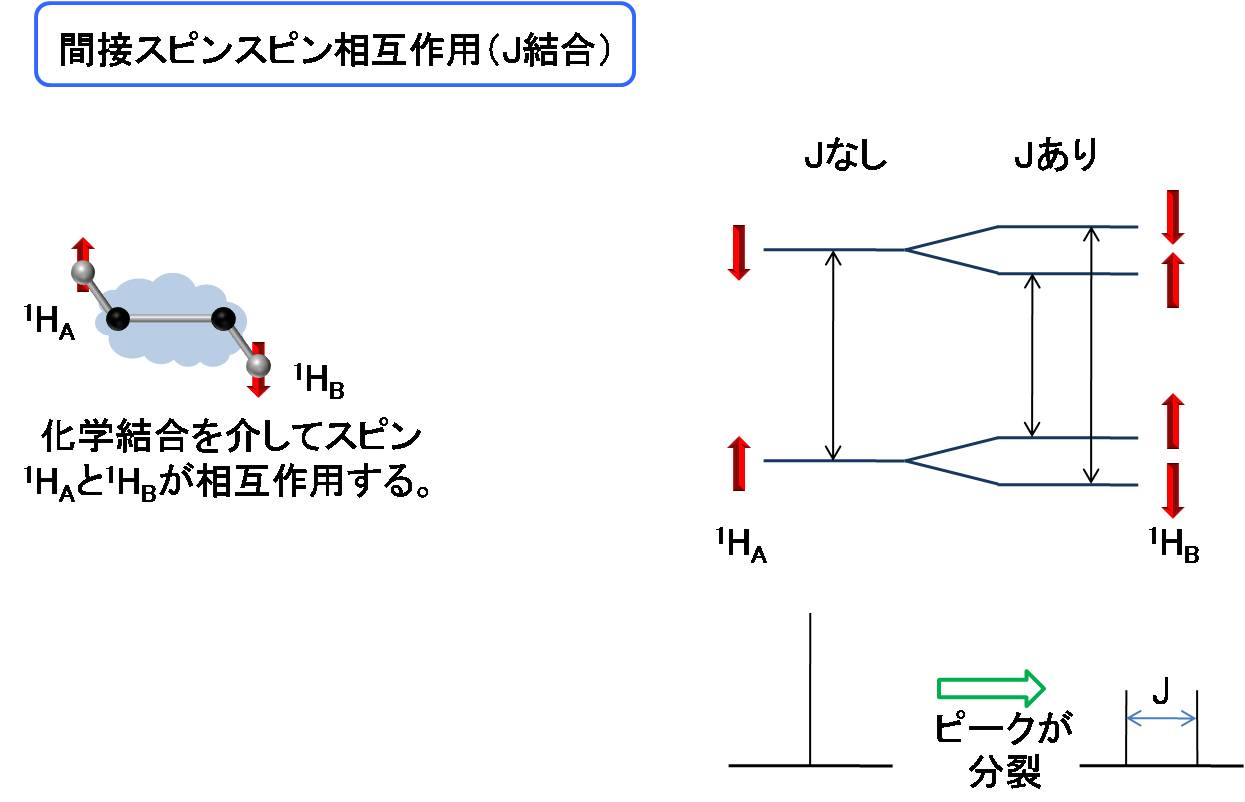
化学結合を介した二つの核スピンの間の相互作用を間接スピンスピン結合と言います。
下の例では、1HAのエネルギー状態は1HB
との相互作用により変化ます。それによりNMRスペクトルのピークは2本に分裂します。
複数のスピンと間接スピンスピン結合していれば、ピークはより多く分裂します。
分裂の仕方から化学結合の様子を知ることができます。
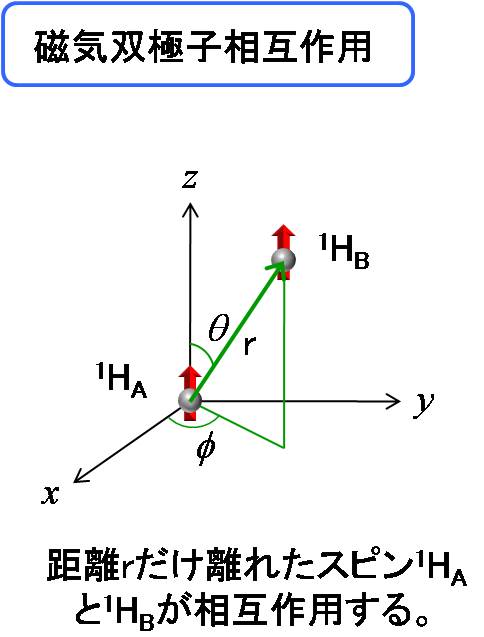
距離rだけ離れた二つの磁気双極子は相互作用します。これを磁気双極子相互作用と言い、
適切な測定を行うことにより核間の距離を知ることができます。
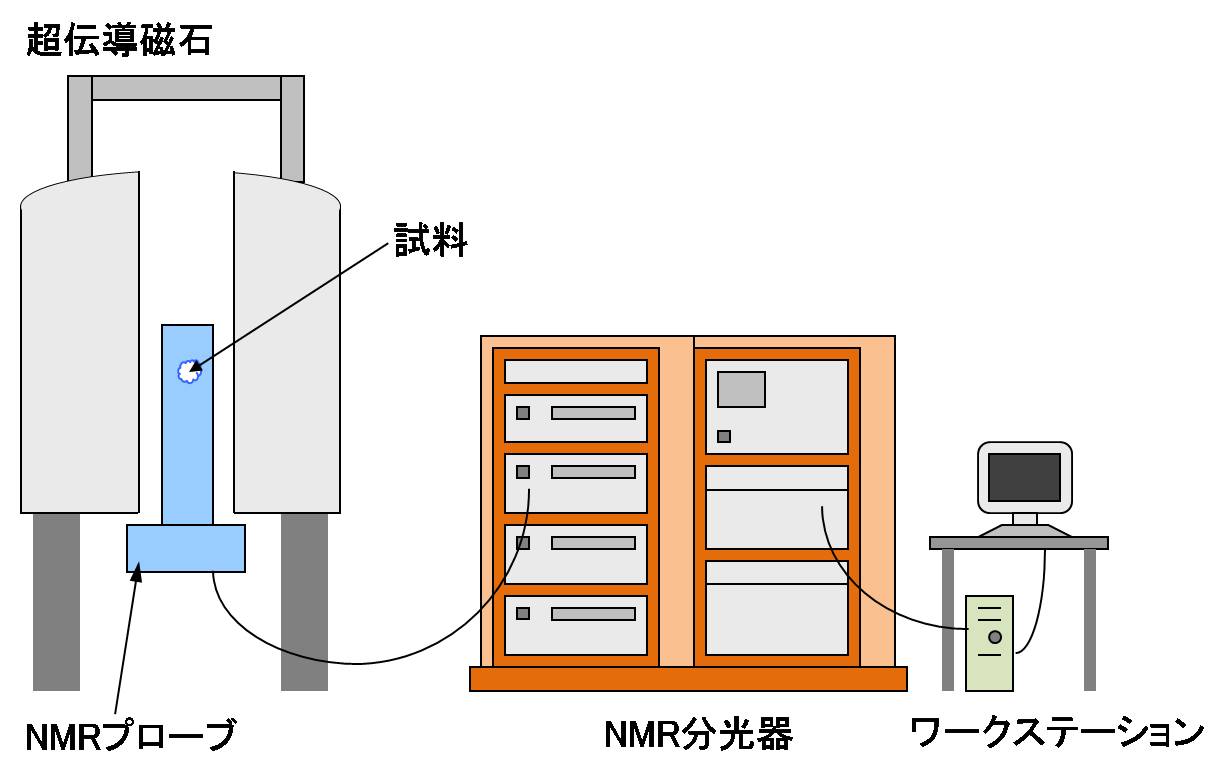
NMRシステムの概要図を以下に示します。NMRでは通常2-20 T程度の磁場を発生させる超電導磁石のボアの中に、 NMRプローブを挿入し測定を行います。NMRの信号を発生・観測するためにNMR分光器を用い、 その分光器はワークステーションで制御します。
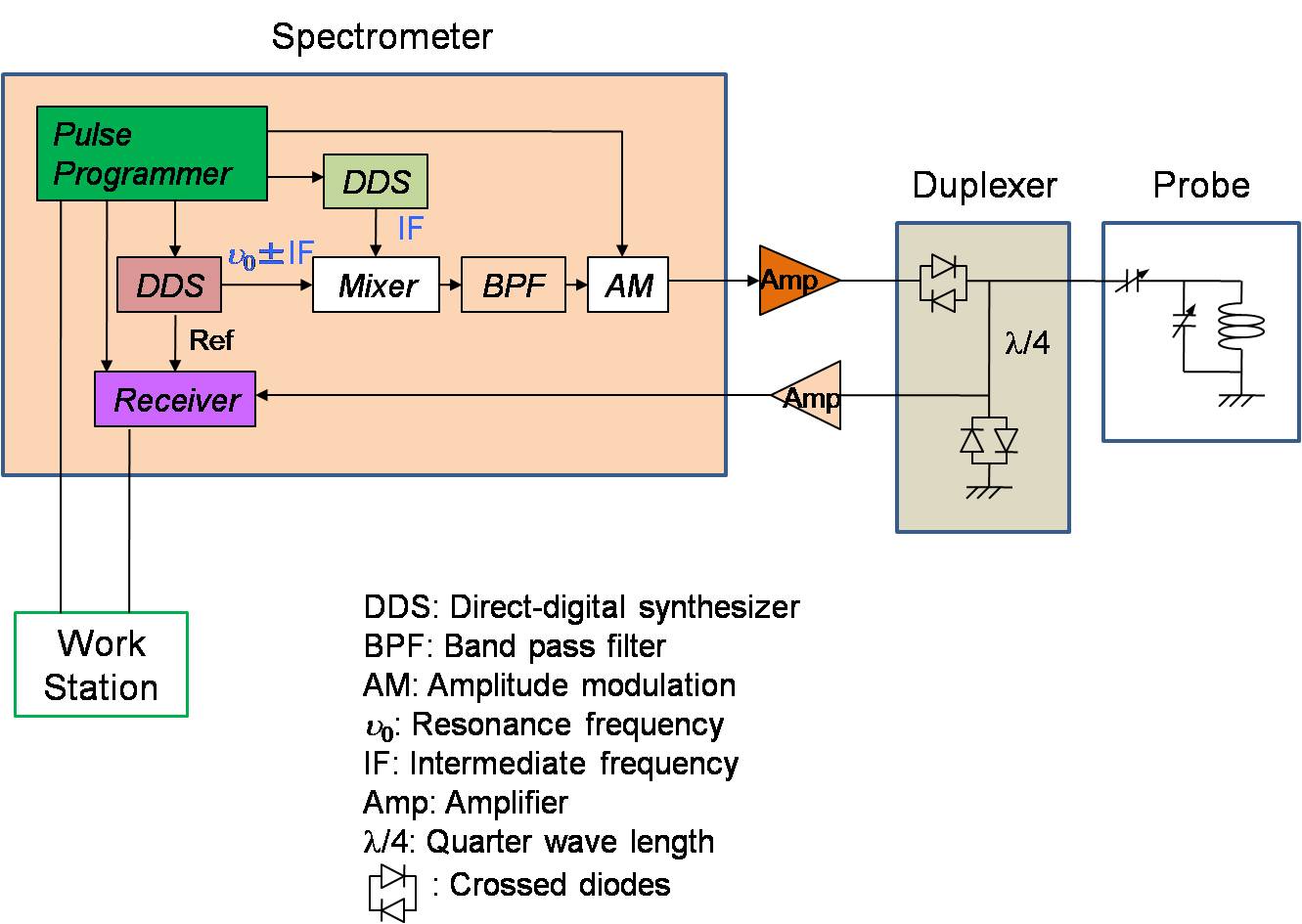
興味ある方のため、もう少し詳細な一重共鳴用のブロック図を以下に示します。 一番左にあるブロックが分光器の内部の構造です。 分光器から出力されたラジオ波をパワーアンプで増幅し、プローブへと送ります。また、 プローブで検出された信号をプリアンプで増幅し、分光器のレシーバへ返します。 アンプとプローブの間にあるのがデュプレクサと言われる入出力スイッチです。 交差ダイオードとλ/4ケーブルを利用し、 ハイパワーのパルスとローパワーのNMR信号を方向づけしています。 プローブは、二つの可変コンデンサを使い、共振周波数でインピーダンス整合(Z = 50 Ω) をとります。コイルの中に試料を入れてNMR測定を行います。
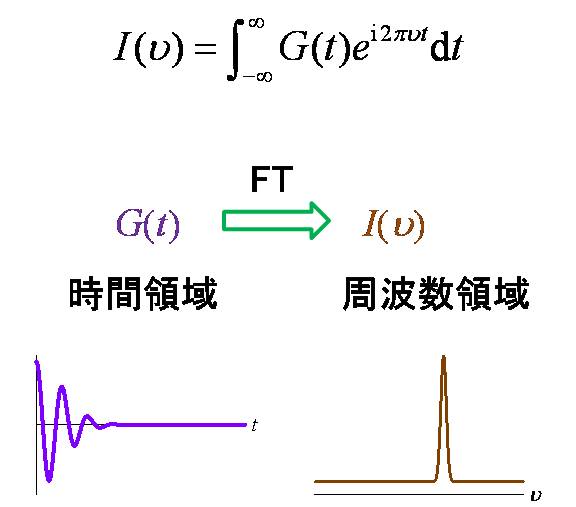
パルスNMRにおいては、NMR信号は時間(t)領域のデータとして得られます。しかし、 時間領域のデータでは、そこに含まれる周波数(ν)の成分を知ることは困難です。 単一成分だけならまだしも、周波数成分が増えるとお手上げです。 そこで、時間領域→周波数領域への変換を行い、直接、周波数成分を 観測します。ここで用いる変換をフーリエ変換(Fourier transform, FT)と言います。
FTのいくつかの重要な特徴・性質を以下で図解説明します。
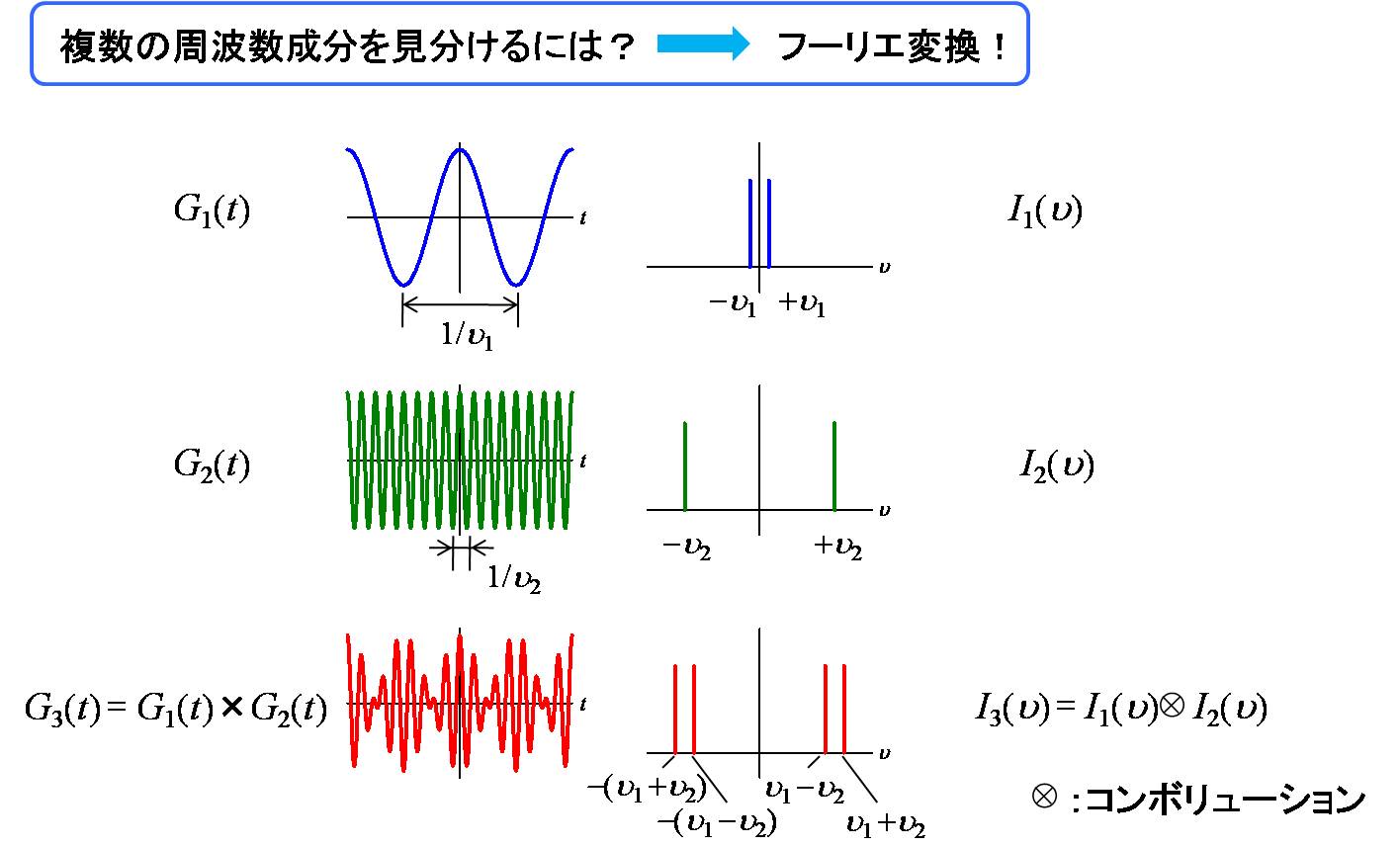
FTが威力を発揮するのは複数の周波数成分が混在している場合です。
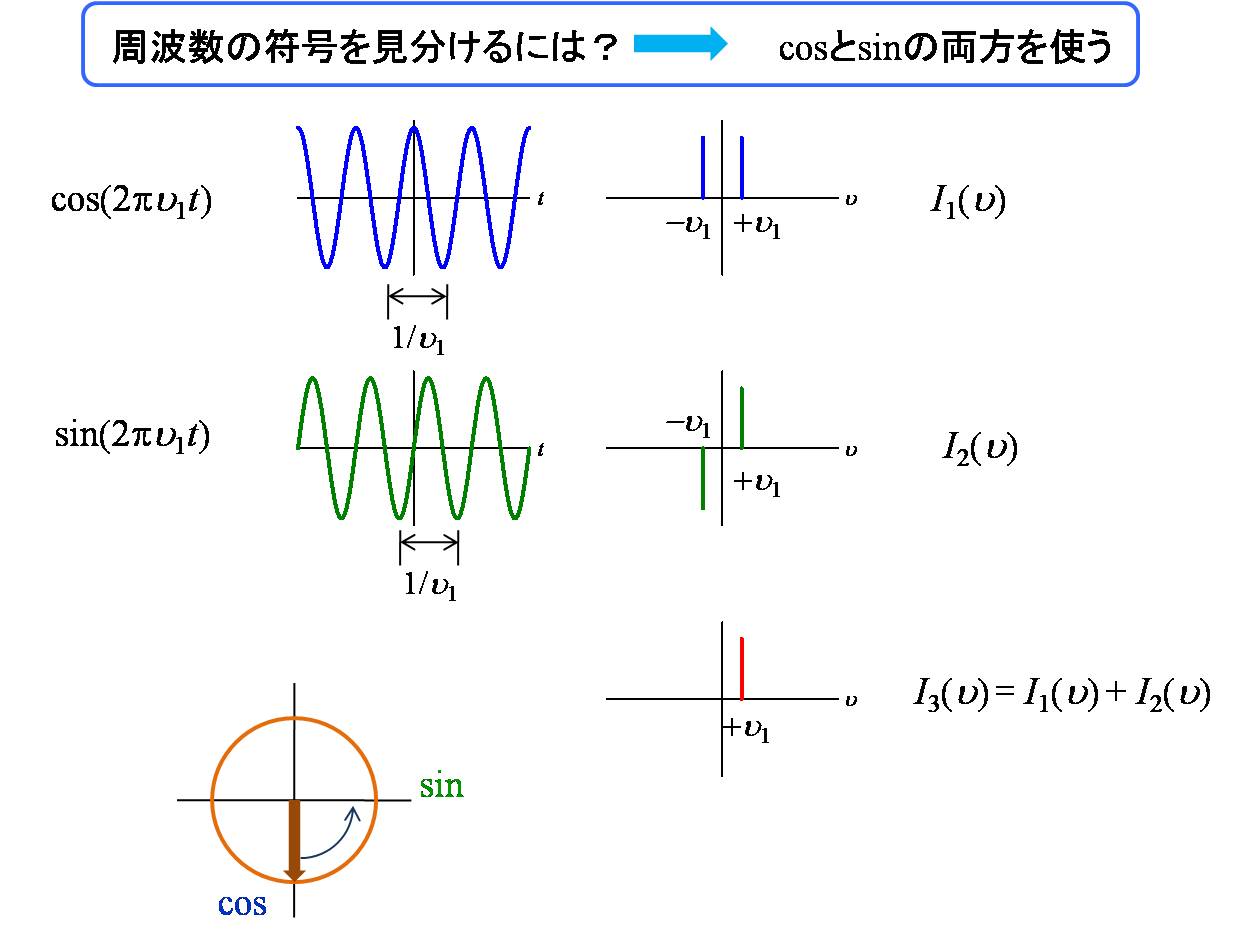
下図の例では、cos関数をFTしています。
ν1とν2が混じった信号G3(t)でも、
FTすれば周波数成分が容易に分かります。
上図のようにcos関数をFTすると、±νにピークが現れ、符号が分かりません。
これを可能にするためにsin関数も利用します。
実際のNMR測定では、90°ずらした二つの参照信号を用いる位相敏感検波を行っています。
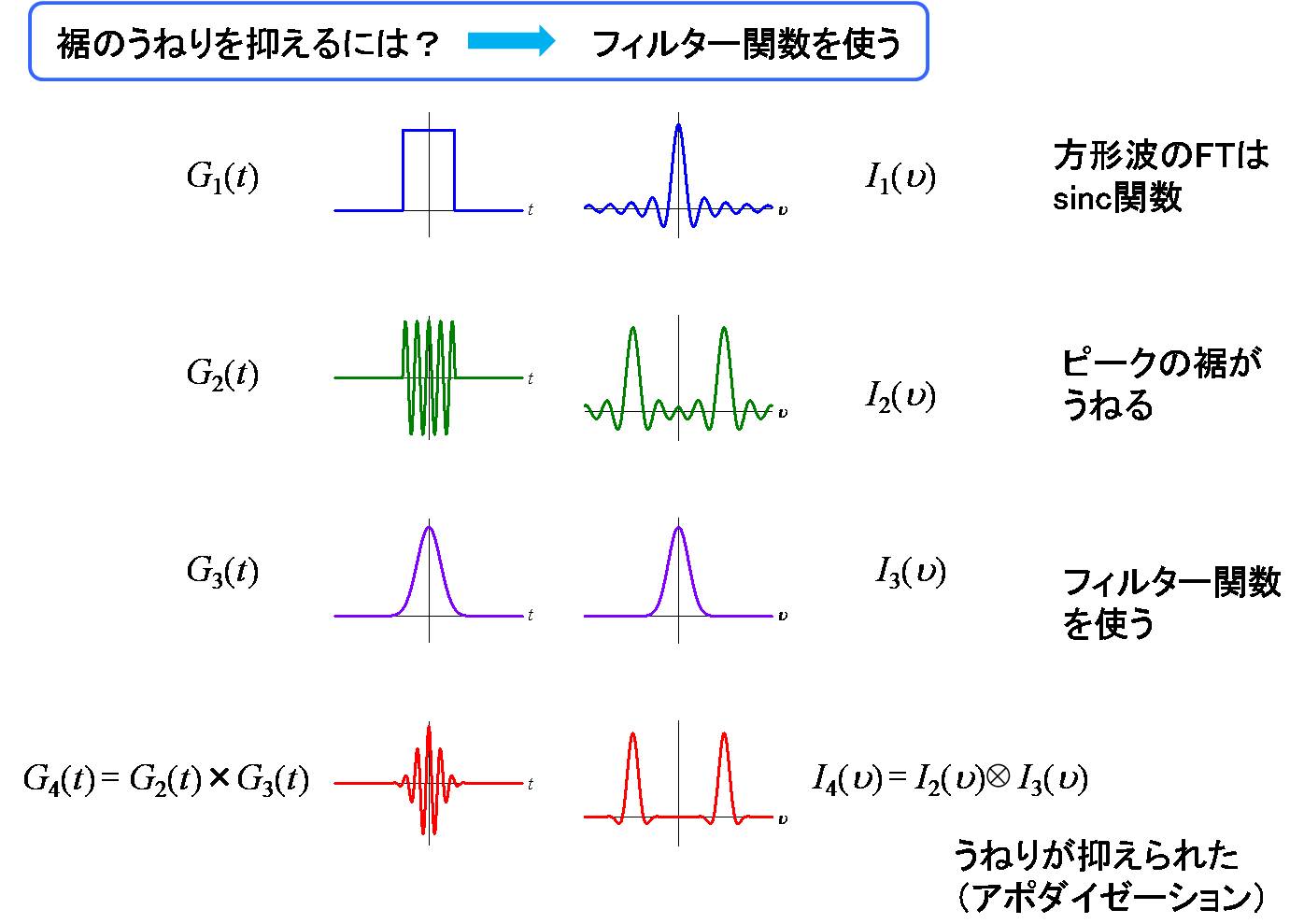
方形波のFTはsinc関数になります。そのため、時間領域の信号が途中で切れている場合は、
FTしたスペクトルの裾にはリップルが現れます。
これを抑制するためにフィルター関数(exponential, gaussian, trapezoid, etc.)を用います。
NMR信号にフィルター関数を掛けることによりスペクトルのリップルが抑えられます(アポダイゼーション)。
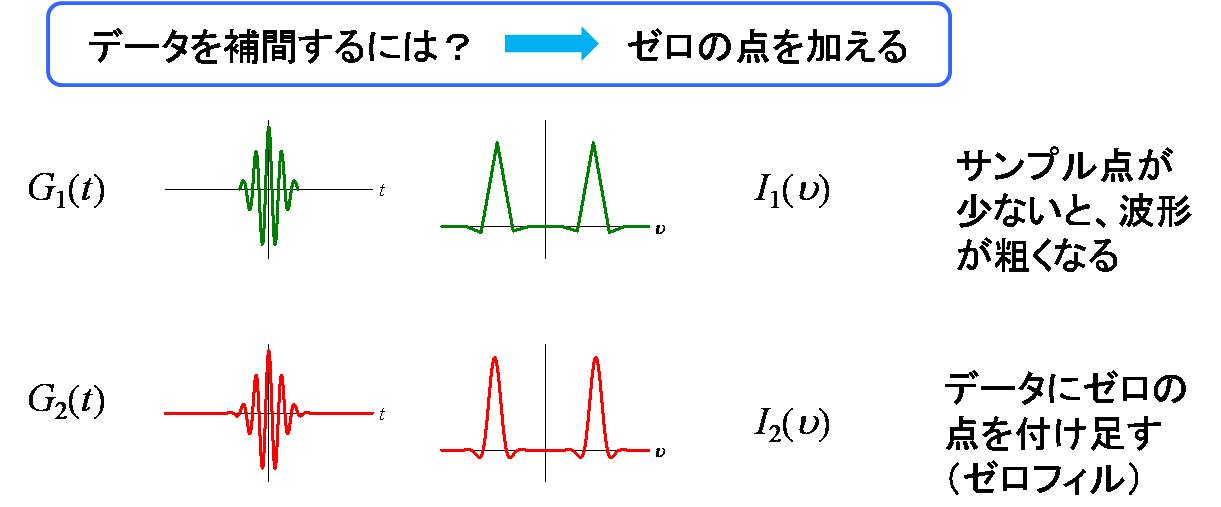
データはどれだけ取り込めば良いのでしょう?
ポイント数が少ないとデータサイズが小さくすみますが、
そのままFTすると波形が粗くなってしまいます。
この波形をデータ補間するために利用するのがゼロフィルという方法です。
これらの性質を利用して、NMR信号を最適に処理してスペクトルを得ます。